Mathematik
Hinweise zu math. Themen © von André Gisler Dipl. Math. ETH ,
Kantonsschule Zug (Gymnasium),
Schweiz
Trigonometrie
Das Winkel-Problem beim Sinus bzw. Arcussinus
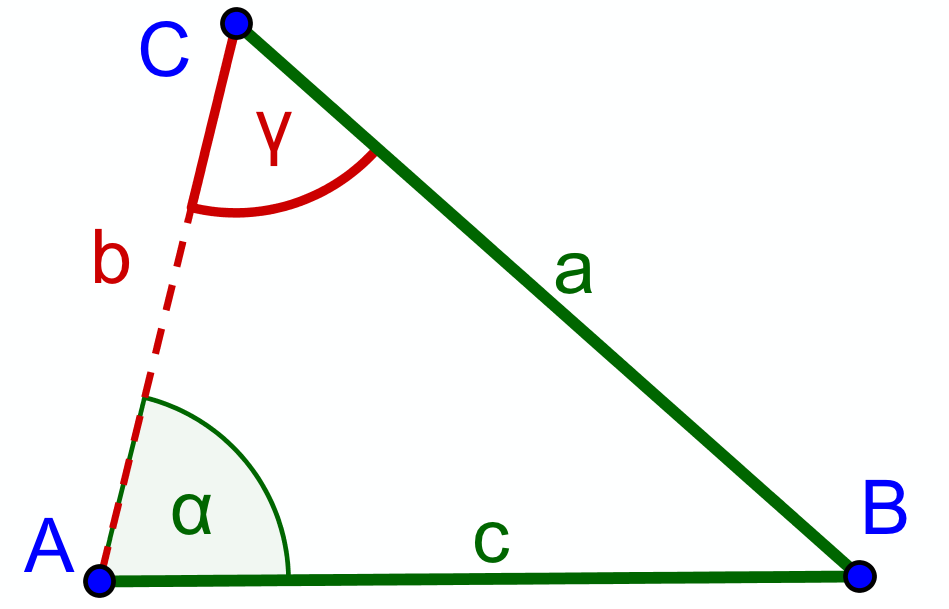
Von einem Dreieck ABC sind gegeben: Die Seiten a, c und der Winkel alpha. Mit dem Sinussatz erhalten wir
Diese Gleichung hat zwei Lösungen für γ (vgl. ArcSin). Welche ist die richtige? |
 |
Überlegung 1
Von den Kongruenzsätzen her erinnerst du dich: Ein Dreieck aus zwei Seiten und einem anschliessenden Winkel ist nur dann eindeutig bestimmt, wenn der Winkel der grösseren Seite gegenüber liegt. Liegt der gegebene Winkel der kleineren der gegebenen Seiten gegenüber, gibt es im Normalfall zwei Lösungen.
Das heisst:
alpha liegt der Seite a gegenüber. Falls a > c ist, besitzt obige Aufgabe nur eine Lösung.
Anderenfalls kann sie zwei Lösungen haben:
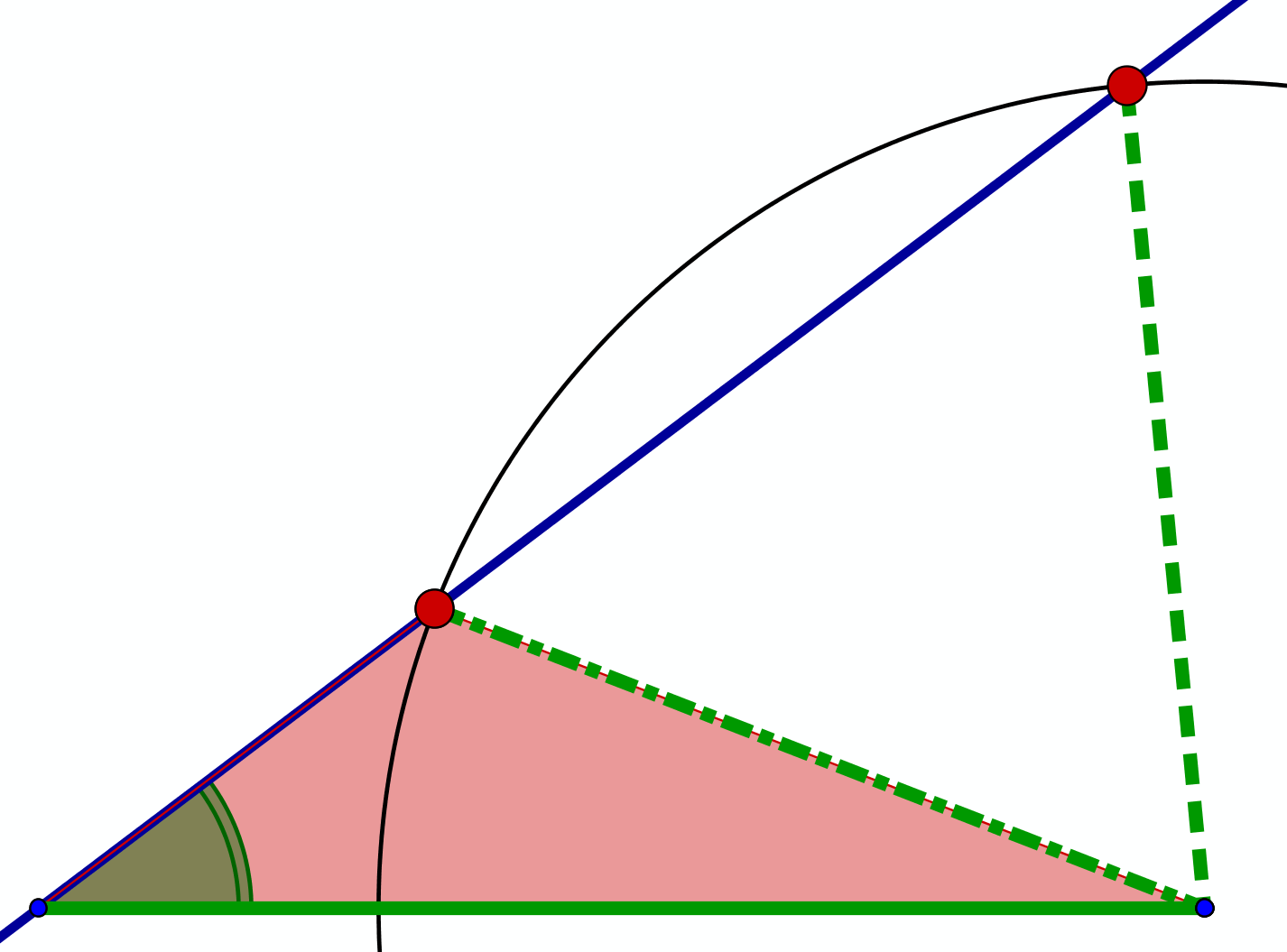
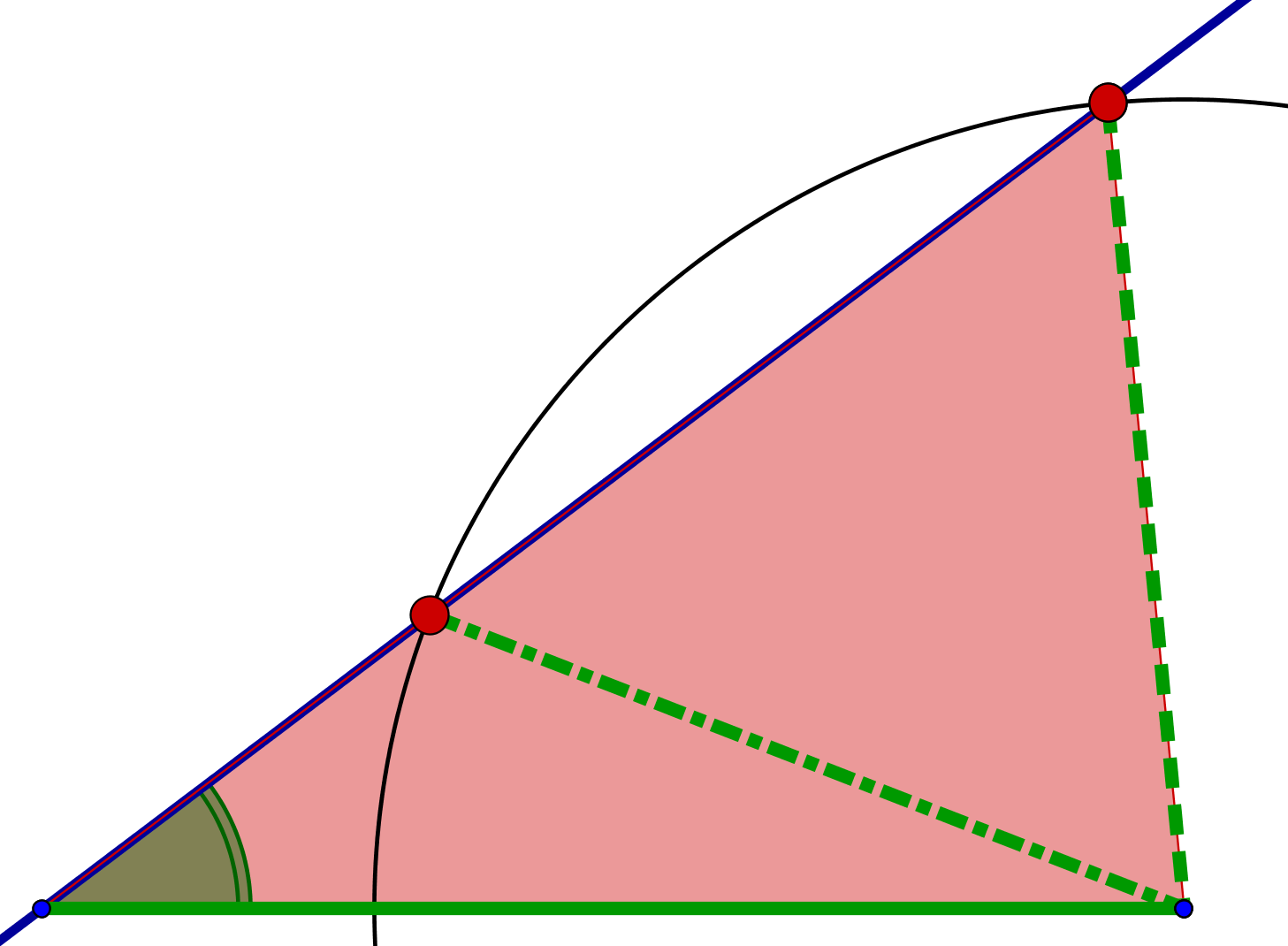
Falls wegen SsW die Aufgabe eindeutig lösbar ist, helfen dir die folgenden Überlegungen:
Überlegung 2
Oft kannst du aufgrund der Winkelsumme im Dreieck die zweite (grössere) Lösung des Winkels ausschliessen.
Nehmen wir zum Beispiel an, der gegebene Winkel alpha sei gleich alpha = 47° .
Für sin(β) hast du 0.5 erhalten → γ1 = 30° γ2 = 150°
Weil die Winkelsumme im Dreieck 180° beträgt, ist γ2 = 150° gar nicht möglich. Folglich ist γ1 = 30° die richtige Lösung für den Winkel γ .
Überlegung 3
In jedem Dreieck gilt die Regel: Der grössten Seite liegt der grösste Winkel gegenüber.
|
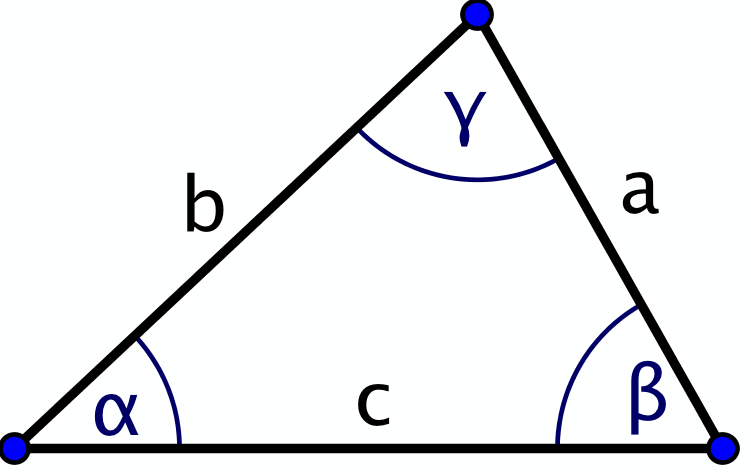 |
| Letzte Änderung: 04.03.2023 |